分类问题
线性回归的内容讨论了如何使用线性模型进行回归学习,并对未来样本做出预测。但是,如果我们要解决分类问题的话,应该怎么做?可不可以利用线性模型来完成分类任务?
利用线性回归解决分类问题
对于二分类问题,一种简单的想法是,我们对一个简单的线性函数设置一个阈值(threshold)。我们使用一个线性函数对样本进行预测,当预测值大于 threshold 时,我们将样本的类别判断为真(或 1 );当预测值小于 threshold 时,我们将样本判断为假(或 0 )。
我们需要将预测值转化为 0/1 值,所以我们可以定义模型为:
$$
y =
\begin{cases}
1 & \quad h_{\theta} \geq 0.5 \
0 & \quad h_{\theta} < 0.5 \
\end{cases}
$$
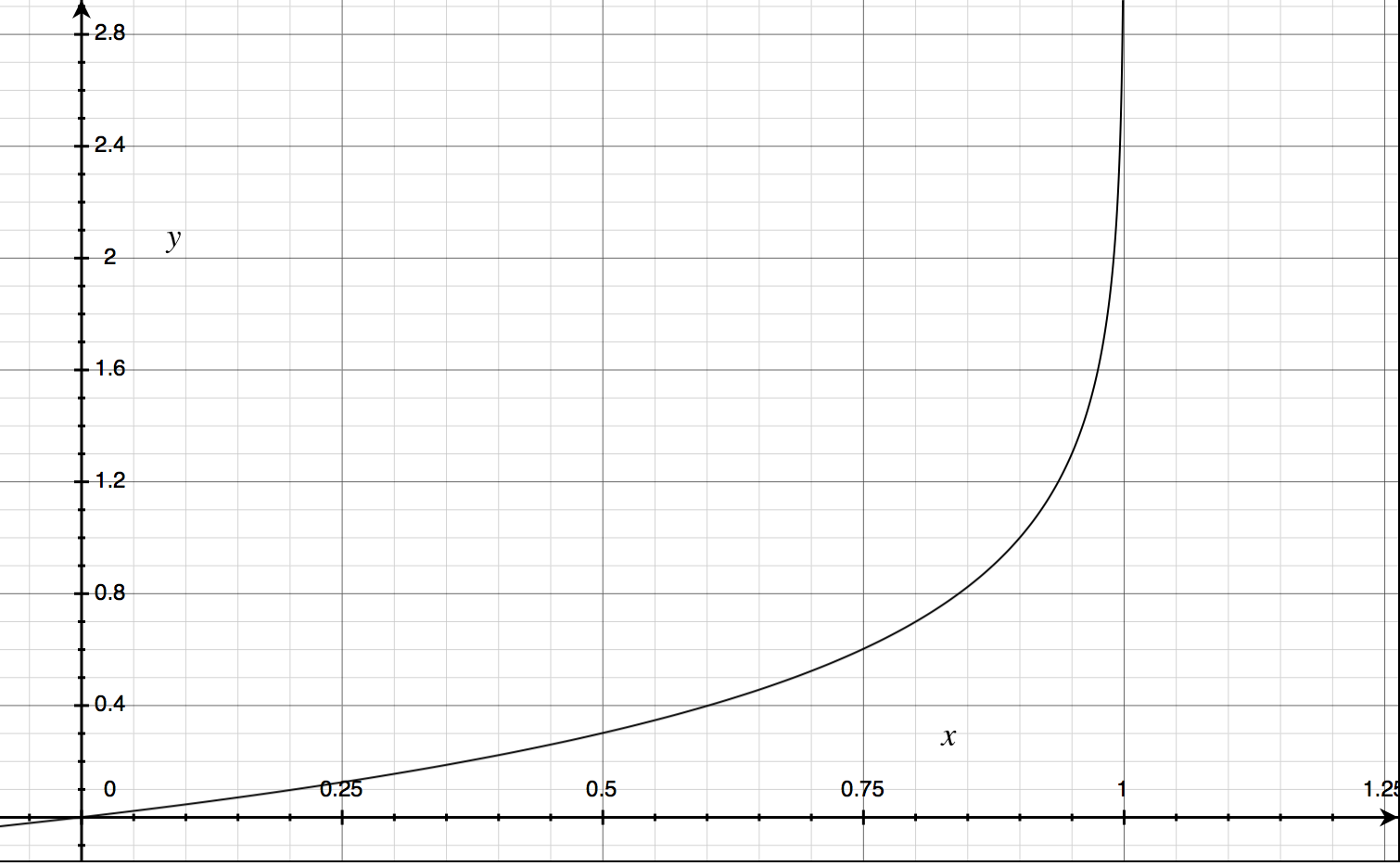
但问题在于这个函数是不可靠的,例如,当我们有6个样本时,我们根据现有样本做线性回归,可以得到如下的拟合曲线:
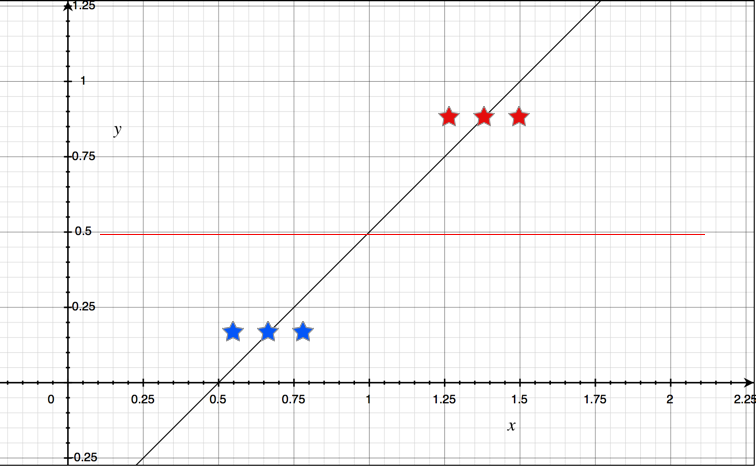
如图,下面的三个样本被判定为假,上面的三个样本被判定为真。但是当样本数量增加时, 我们的拟合曲线可能会造成判断错误,出现较大的误差。
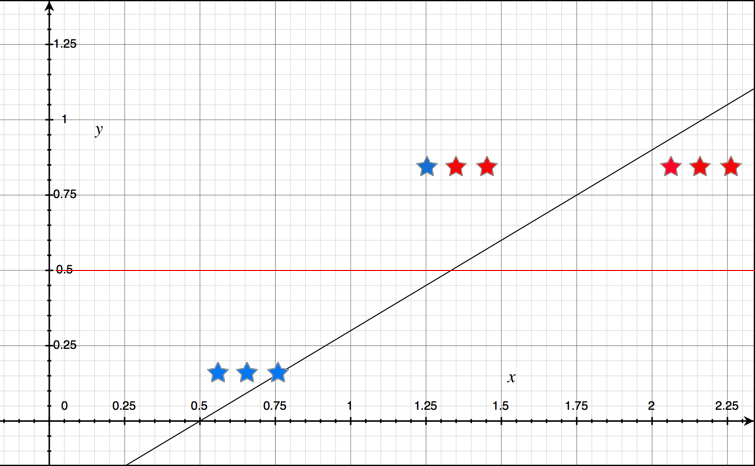
我们根据新的9个样本进行线性回归,到得到的新的回归曲线。在 $x = 1.25$ 处的样本,它的值大于0.5,应该被判断为真;但是新的回归曲线在该点的函数值小于0.5,所以该样本会被错误地判断为假。
所以,单纯地使用线性回归方法实现二分类是不合适的。
Sigmoid 函数
我们可以使用 Sigmoid 函数,它有非常良好的数学性质,例如:单调可微,在 $0 \dots 1$ 之间变化等。Sigmoid 函数的表达式为: $$ y = \frac{1}{1 + \mathrm{e}^{-\mathrm{z}}} $$
它的函数图形为:
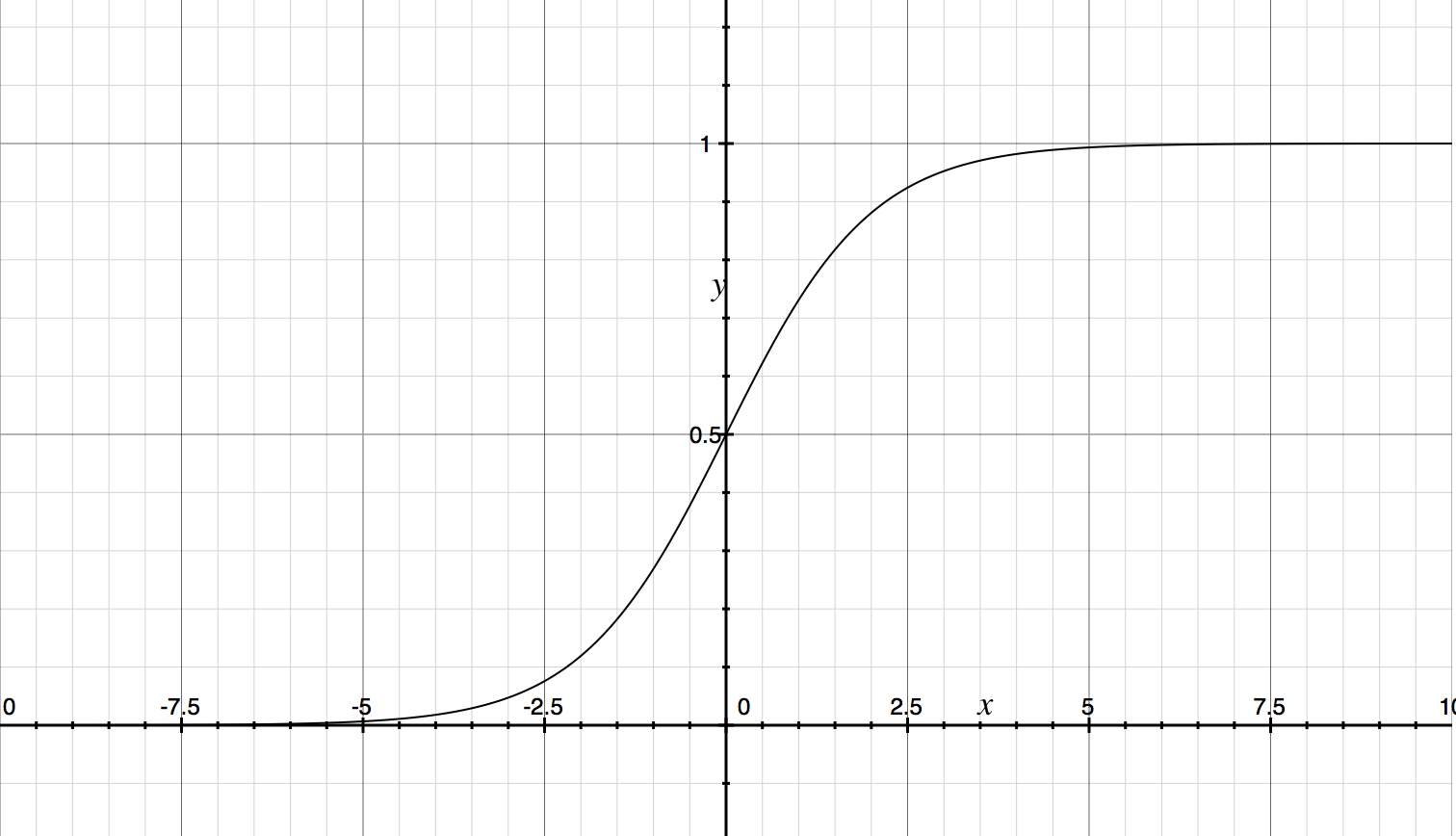
在有了 Sigmoid 方程后,我们可以令 $ z = \theta^{T}x $。也可以得到:
$$ y = \frac{1}{1 + e^{-\theta^{T}x}} $$
即:
$$ ln\frac{y}{1-y} = \theta^{T}x $$
我们可以将 $y$ 看做样本 $x$ 为正例的可能性,将 $1 - y$ 看做样本 $x$ 为反例的可能性。也就是说,我们是在用线性回归模型的预测结果去逼近真实标记的对数几率。所以,这个模型被称为“对数几率回归”(Logistic Regression)。
在这个模型中,我们是直接对分类可能心进行建模,而且无需实现假设分布,这样就可以避免假设分布不准确所带来的问题;它不是仅仅预测出“类别”,而是可以得到近似的概率预测;最后,Sigmoid 函数是一种任意阶可导的凸函数,有很多数值计算方法可以用来求取最优解。
Cost Function
对于线性回归模型,我们定义的代价函数(Cost Function)是所有模型误差的平方和。理论上讲,我们可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将 $ h_{\theta} = \frac{1}{1 + e^{-\theta^{T}x}} $ 带入到代价函数中时,我们得到的代价函数将是非凸函数(non-convex function)。这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
所以,我们重新定义逻辑回归的代价函数为:
$$J(\theta) = \frac{1}{m}\sum_{1}^{m}Cost(h_{\theta}(x^{(i)}, y^{(i)}))$$
其中:
$$ Cost(h_{\theta}, y) =
\begin{cases}
-log(h_{\theta}(x)) & \quad y = 1 \
-log(1 - h_{\theta}(x)) & \quad y = 0 \
\end{cases}
$$
$h_{\theta}(x)$与$Cost(h_{\theta}(x), y)$之间的关系如下图所示:
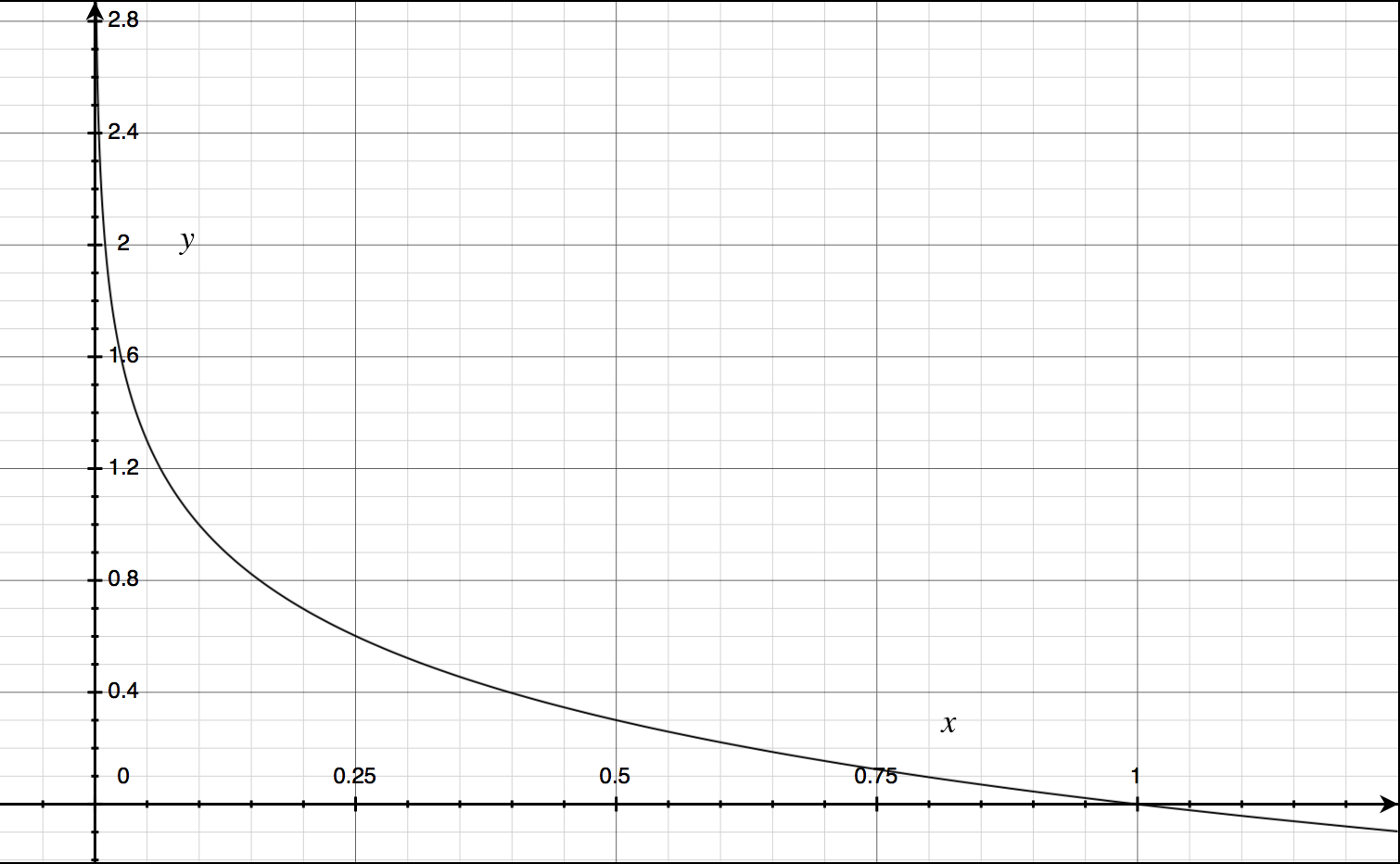
这样构建的 $Cost(h_{\theta},y)$ 的特点是:当实际的$y=1$且$h_{\theta}$也为1时误差为0,当$y = 1$但$h_{\theta}$不为1时,误差随着$h_{\theta}$的变小而变大;当实际的$y = 0$且$h_{\theta}$也为0时,代价为0,当$y=0$但$h_{\theta}$不为0时,误差随着$h_{\theta}$的变大而变大。
这样,我们可以得到简化后的 $Cost(h_{\theta}(x), y)$:
$$ Cost(h_{\theta}(x),y) = -ylog(h_{\theta}(x))-(1-y)log(1-h_{\theta}(x))$$
带入代价方程我们可以得到:
$$
J(\theta) = -\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})og(1-h_{\theta}(x))]
$$
有了这样一个代价函数后,我们就可以使用梯度下降的算法来求得能使代价最小的参数了。
优化
查了梯度下降算法外,我们还可以使用一些常常被用来计算最小代价的算法,这些算法更加复杂和优越,而且不需要人工干预学习率,且比梯度下降算法更加快速。比如:Conjugate Gradient, BFGS, L-BFGS等。我们在实现求解 Logistic Regression 的参数的时候,可以跟根据自己所使用的语言或平台来利用这些函数,从而实现快速、高效的参数学习。
多分类问题
在多分类问题中,我们要训练的样本属于多个类,我们无法使用二元变量对这些类别进行区分。例如,我们要预测一个学生的学习情况,可分为:差、良和优秀。一种解决多分类问题的方法被称为 “One-vs-All” 算法。
One-vs-All
使用 “One-vs-All” 方法,我们将多分类问题,转化为二分类问题。为了实现这样的转变,我们将其中的一个类标记为正类($y = 1$),其他所有类别标记为负类,这个模型被记作$h_{\theta}^{(1)}(x)$。接着类似地我们将另外一个类选择为正类($y=2$),其他类别标记为负类,这个模型被记作$h_{\theta}^{(2)}(x)$。以此类推。
我们可以得到分类器模型:$h_{\theta}^{(i)}=p(y=i|x;\theta) \quad i \in [1 \dots k]$。
在预测中,我们要运行每一个分类器,并对每一个输入变量,都选择最高可能性的输出变量。
过度拟合问题(Overfitting)
如果我们的模型中有数目过多的属性,那么我们通过学习所得到的属性可能会非常好得适应训练样本(代价函数的值几乎为0),但是可能无法推广到新的样本中。
如果我们遇到了过拟合问题,一般有两种方法:
- 减少属性数目
可以是手工选择保留那些属性,也可以运行某些属性选择算法。 - 归一化(Regularization)
保留所有的属性,但是减少某些属性的重要性(Magnitude)。当我们有很多对预测结果有略微作用的属性时,归一化的效果非常好。
Regularization
Regularization - Cost Funtion
例如在某问题中,我们的预测模型为:
$$ h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}^{2}+\theta_{3}x_{3}^{3}+\theta_{4}x_{4}^{4} $$
我们决定减少$\theta_3$和$\theta_4$的作用,要做得就是修改代价函数,为$\theta_3$和$\theta_4$设置一点惩罚。这样的话,我们在尝试最小化代价函数的同时,也需要将这个惩罚纳入考虑中,修改后的代价函数可以是:
$$
min_{\theta}\frac{1}{2m}\sum_{i=1}^{m}((h_{\theta}(x^{(i)})-y^{(i)})+1000\theta_{3}^{2}+10000\theta_{4}^{2})
$$
通过这样的代价函数,我们选择得出的$\theta_{3}$和$\theta_{4}$对预测结果的影响要比之前小得多。
假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设:
$$
J(\theta)=\frac{1}{2m}\big[\sum_{i=1}^{m}((h_{\theta}(x^{(i)})-y^{(i)})^{2})+\lambda\sum_{j=1}^{n}{\theta}_{j}^{2} \big]
$$
注意:我们不对$\theta_{0}$进行惩罚。
但是如果选择归一化参数$\lambda$过大的话,则会把所有参数的作用都减小,可能造成欠拟合。
Regularized Linear Regression
归一化的线性回归代价函数为:
$$
J(\theta)=\frac{1}{2m}\big[ \sum_{i=1}^{m}((h_{\theta}(x^{(i)})-y^{(i)})^{2}+\lambda\sum_{j=1}^{m}\theta_{j}^{2}) \big]
$$
如果我们采用梯度下降来实现这个代价函数的最小化,因为我们没有对$\theta_0$进行归一化,所以梯度下降算法将分为两种情形:
$$
\quad \theta_0=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^{m}\big[ h_{\theta}(x^{(i)})-y^{(i)} \big]x_{0}^{(i)} \
\quad \theta_{j}=\theta_{j}-\alpha\bigg[ \big[\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)} \big]+\frac{\lambda}{m}\theta_{j} \bigg] \
j \in [1 \dots n]
$$
对上式变化可得:
$$
\theta_j=\theta_{j}(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}
$$
我们可以看到,归一化方程的梯度下降算法就是在每次迭代过程中,令$\theta$减少一个额外的值。
Normal Equation
我们也可以使用正规方程来求解归一化线性回归模型:
$$
\theta = ( X^{T}X - {\lambda}L )^{-1}X^{T}y
$$
其中:
$$
L =
\begin{bmatrix}
0 \
\quad & 1 \
\quad & \quad & \ddots \
\quad & \quad & \quad & 1 \
\end{bmatrix}_{(m+1) \times (n+1)}
$$
注意:如果$X^{T}X$不可逆,则$X^{T}X+{\lambda}L$也不可逆。
错题集锦
下面是我在完成课程的小测验过程中的错题,我将相关知识点罗列如下:
- 在模型中添加新的属性仅仅可以提高在训练集上的匹配程度。
- 在$m \geq 1 $个样本上训练得到的 Logistic Regression 代价函数一定大于等于1.
- Logistic Regression 的代价函数是“凸函数”,所以梯度下降算法一定会达到全局最优点。但是我们依然可能选择使用优化算法,因为这些算法可以更加高效地习得模型的最佳参数,并且不需要我们选择 Learning Rate。
- 通过添加新的属性,我们的模型一定会更加精确地表达样本的特点,从而可以习得更加复杂的假设来匹配训练样本。
- 当$\lambda$被设为1时,我们使用归一化来减少$\theta$的值。这样,$\theta$会更小。
- 归一化通过“惩罚”参数的作用,可能会实现一个更简单的模型,会分类错误更多的样本。
- 如果算法在一个训练样本上的分类效果很差的话,这意味着模型处于欠拟合状态。这种情况下,以应该通过增加属性数量、使用多项式回归等方法来提高模型的性能。
参考文献
- 机器学习 周志华
- Machine Learning Stanford